FTRL

参考：http://vividfree.github.io/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0/2015/12/05/understanding-FTRL-algorithm

http://iyao.ren/?p=137

1. 引言

在工业界，越来越多的业务需要大规模机器学习，不单参与训练的数据量大，模型特征量的规模也大。例如点击率预估，训练数据量在TB量级，特征量在亿这个量级，业内常用LR（Logistic Regression）和FM（Factorization Machines）为点击率预估建模。对LR、FM这类模型的参数学习，传统的学习算法是batch learning算法，它无法有效地处理大规模的数据集，也无法有效地处理大规模的在线数据流。这时，有效且高效的online learning算法显得尤为重要。

SGD算法[1]是常用的online learning算法，它能学习出不错的模型，但学出的模型不是稀疏的。为此，学术界和工业界都在研究这样一种online learning算法，它能学习出有效的且稀疏的模型。FTRL（Follow the Regularized Leader）算法正是这样一种算法，它由Google的H. Brendan McMahan在2010年提出的。

FTRL算法融合了RDA算法能产生稀疏模型的特性和SGD算法能产生更有效模型的特性。它在处理诸如LR之类的带非光滑正则化项（例如1范数，做模型复杂度控制和稀疏化）的凸优化问题上性能非常出色，国内各大互联网公司都已将该算法应用到实际产品中。

2. FTRL算法与SGD算法的联系

SGD算法的迭代计算公式如下： $\mathbf{w_{t+1}} = \mathbf{w}_t− \eta_t\mathbf{g}_t$

其中 $t$ 为迭代轮数，$\mathbf{w}$是模型参数，$\mathbf{g}$是loss function关于$\mathbf{w}$的梯度，而$η$是学习率，它随着迭代轮数增多而递减。

FTRL算法的迭代算公式如下： $\mathbf{w}_{t+1}=\mathop{\arg\min}_{\textbf{w}} (\sum_{s=1}^t \textbf{g}_s\cdot \mathbf{w} + \frac{1}{2}\sum_{s=1}^t \sigma_s ||\mathbf{w}−\mathbf{w}_s||_2^2+ \lambda_1||\mathbf{w}||_1)$ 其中 $t$ 为迭代轮数，$\mathbf{w}$是模型参数，$\sigma_s$定义成$\sum_\limits{s=1}^t \sigma_s = \frac{1}{\eta_t}$，$\lambda_1$是L1正则化系数。

公式2看似比公式1复杂，需要求最优解，但其实很容易算出$w_{t+1}$的close form表达式，详见文章[4]。在公式2中，arg min算子的内容中由3项组成，最后一项是L1正则（当然也可以再加上L2正则），很明显L1正则是为了获取稀疏模型。如果令$\lambda_1=0$，也就是说不要正则项。此时FTRL完全等价于SGD（是等价，不是近似）。推导见参考材料。

3. FTRL原理介绍

FTRL算法的设计思想其实并不复杂，就是每次找到让之前所有目标函数（损失函数加正则项）之和最小的参数。

该算法在处理诸如逻辑回归之类的带非光滑正则化项（如L1正则项）的凸优化问题上表现出色，在计算精度和特征的稀疏性上做到了很好的trade off，而且其在工程实现上做了大量优化，性能优异。

在介绍FTRL原理之前，首先介绍一些online learning凸优化算法的设计理念：

正则项：众所周知，目标函数添加L1正则项可增加模型解的稀疏性，添加L2正则项有利于防止模型过拟合，当然，也可以将两者结合使用，即混合正则，并且FTRL就是这样设计的。
稀疏性：模型解的稀疏性在机器学习中是很重要的事情，尤其是在工程应用领域，稀疏的模型解会大大减少预测时的内存和时间复杂度。常用的稀疏性方法包括：加入L1正则项（但其效果有限），Truncated Gradient（通过一些策略，将符合条件的特征权重强置为0，如后文介绍的FOBOS就采用了类似这种方式），黑箱测试法（除去部分特征，重新训练模型，以实验被消去的特征是否有效）。
GD/SGD：如前所述，GD求解的模型虽然精度相对较高，但具有训练太费时、不易得到稀疏解和对不可微点迭代效果欠佳等缺点；SGD则存在模型解的精度低、收敛速度慢和很难得到稀疏解的缺点。虽然学术界提出了很多加快收敛或者提高模型精度的方法（如添加momentum项、添加nesterov项、Adagrad算法[2]、Adadelta算法[3]、GSA算法[4]等），但这些方法在提高模型解的稀疏性方面效果有限，而FTRL在这方面则更加有效。

3.2 FOBOS与RDA

FTRL综合了这两个算法的优点，理解了这两个算法将有助于理解FTRL。

3.2.1 FOBOS

该算法是对投影次梯度（projected subgradient）方法的一个改造，以有效的获得模型的稀疏解。该算法将迭代投影次梯度法拆成两步：

3.2.2 RDA

RDA算法于2010年由微软提出，该算法相对与FOBOS在精度与稀疏性之间做了平衡，在L1正则下，RDA相较FOBOS可以更有效地得到稀疏解。RDA的权值迭代公式如下：

3.3 FTRL原理

全名为Per-coordinate Follow The Regularized Leader Proximal。

FTRL融合了RDA和FOBOS的特点，实验表明，在L1正则下，稀疏性与精度都好于RDA和FOBOS。具体实现对比如下：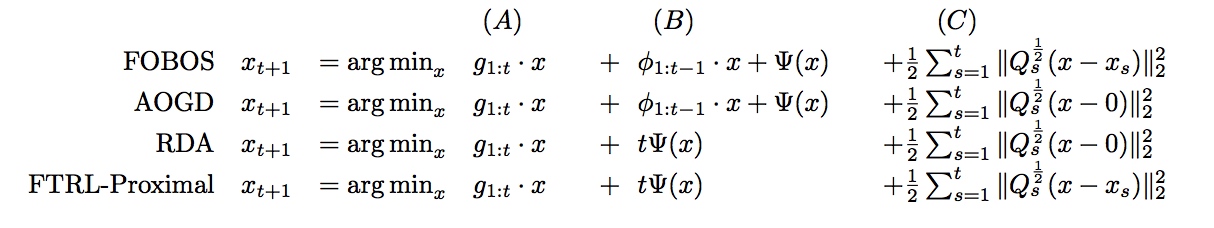

其中（A）代表累积梯度项，（B）代表正则化处理项，（C）代表累加和项（该项限制了新的迭代结果不要与之前的迭代结果偏离太远，也就是FTRL算法中proximal的含义）。

FTRL工程实现部分在理论推导公式的基础上做了一些变换和在工程实现上做了一些trick。其中最值得说明的一点为per-coordinate，即F**TRL是对权重向量w的每一维分开训练更新的，**每一维使用不同的学习速率。

3.4 工程实现的一些经验

下面介绍为FTRL准备训练数据（特征工程）和训练模型时的一些trick。

Raw样本数据预处理
- 样本去重
- 噪声数据过滤
特征工程
- 特征预处理：ID化、离散化、归一化、贝叶斯平滑等；
- 特征选择：方差、变异系数、相关系数、Information Gain、Information Gain-Ratio、IV值等；
- 特征交叉和组合特征：根据特征具有的业务属性特征交叉，利用FM算法、GBDT算法做高维组合特征等。
Subsampling Training Data
- 正样本全采样，负样本使用一个比例r采样，并在模型训练的时候，对负样本的更新梯度乘以权重1/r;
- 负采样的方式：随机负采样、Negative Sampling、邻近负采样、skip above负采样等。
在线丢弃训练数据中很少出现的特征(probabilistic feature inclusion)
- Poisson Inclusion：对某一维度特征所来的训练样本，以p的概率接受并更新模型；
- Bloom Filter Inclusion：用bloom filter从概率上做某一特征出现k次才更新。

4. FTRL与SGD比较

FTRL和RDA是积累每次迭代的梯度： $G^{1:t}\cdot W$ FOBOS只利用上一次迭代的梯度。而不累积： $G^{(t)} \cdot W$ FTRL和FOBOS每次迭代都保证和上一次的迭代结果距离不会太远： $\frac{1}{2} \sum_{s=1}^t ||\mathbf{w}- \mathbf{w}_s||_2^2$ RDA则保证了迭代结果不会距离0太远： $\frac{1}{2} \sigma ^{(1:t)} ||W - 0||_2^2$ 稀疏：截断，即设定阈值，小于阈值的设为0；L1正则算出来的，由于有浮点运算影响，难以达到严格为零。

有效稀疏：：所谓有效稀疏，就是要避免某个权重还没训练充分就被稀疏成0，这时候，累计梯度的作用就出来了，这保证了某权重被训练到一定程度了，才开始稀疏。

SGD为啥不行？稀疏手段还是次要的，主要还是没有做有效稀疏，而有效稀疏的关键是累计梯度。